神经网络学习笔记

MLP

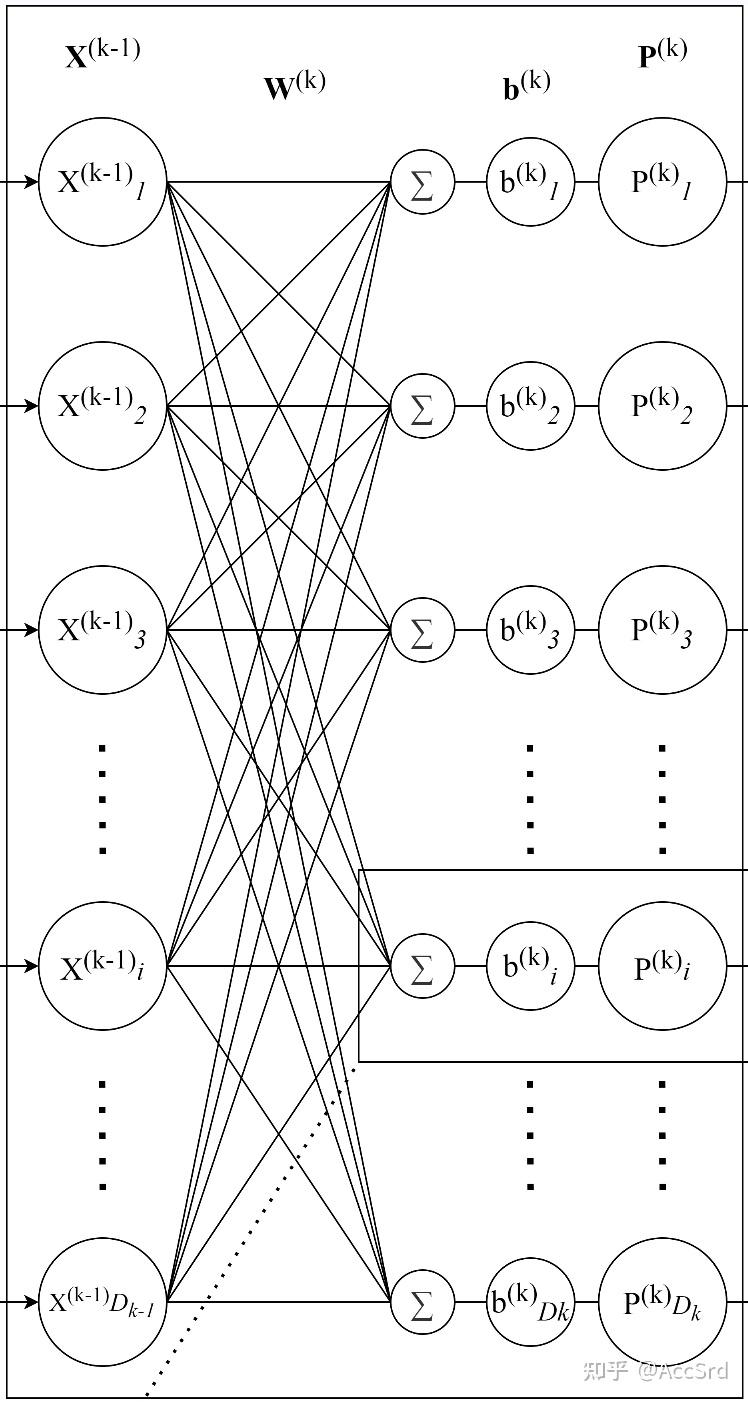
对于 nn 层全连接神经网络（MLP），

  • Xk−1,Wk,bk,Pk\mathbf{X}^{k-1},\mathbf{W}^k,\mathbf{b}^k,\mathbf{P}^k 分别表示第 kk 层全连接网络的输入向量、权重矩阵、偏置向量与隐藏层中间向量

Xk:=[X1kX2k⋮XDkk]Dk×1, Wk:=[W1,1kW1,2k⋯W1,Dk−1kW2,1kW2,2k⋯W2,Dk−1k⋮⋮⋱⋮WDk,1kWDk,2k⋯WDk,Dk−1k]Dk×Dk−1, bk:=[b1kb2k⋮bDkk]Dk×1\mathbf{X}^k:=\begin{bmatrix} X_1^k\\ X_2^k\\ \vdots\\ X_{D_k}^k\\ \end{bmatrix}_{D_k\times1},\ \mathbf{W}^k:=\begin{bmatrix} W_{1,1}^k&W_{1,2}^k&\cdots&W_{1,D_{k-1}}^k\\ W_{2,1}^k&W_{2,2}^k&\cdots&W_{2,D_{k-1}}^k\\ \vdots&\vdots&\ddots&\vdots\\ W_{D_k,1}^k&W_{D_k,2}^k&\cdots&W_{D_k,D_{k-1}}^k\\ \end{bmatrix}_{D_k\times D_{k-1}},\ \mathbf{b}^k:=\begin{bmatrix} b_1^k\\ b_2^k\\ \vdots\\ b_{D_k}^k\\ \end{bmatrix}_{D_k\times1}

当采用 Batch（同时训练多个数据）进行训练时：

Xk:=[X1b1kX1b2k⋯X1bDbkX2b1kX2b2k⋯X2bDbk⋮⋮⋱⋮XDkb1kXDkb2k⋯XDkbDbk]Dk×Db\mathbf{X}^k:=\begin{bmatrix} X_{1b_1}^k&X_{1b_2}^k&\cdots&X_{1b_{D_b}}^k\\ X_{2b_1}^k&X_{2b_2}^k&\cdots&X_{2b_{D_b}}^k\\ \vdots&\vdots&\ddots&\vdots\\ X_{D_kb_1}^k&X_{D_kb_2}^k&\cdots&X_{D_kb_{D_b}}^k\\ \end{bmatrix}_{D_k\times D_b}

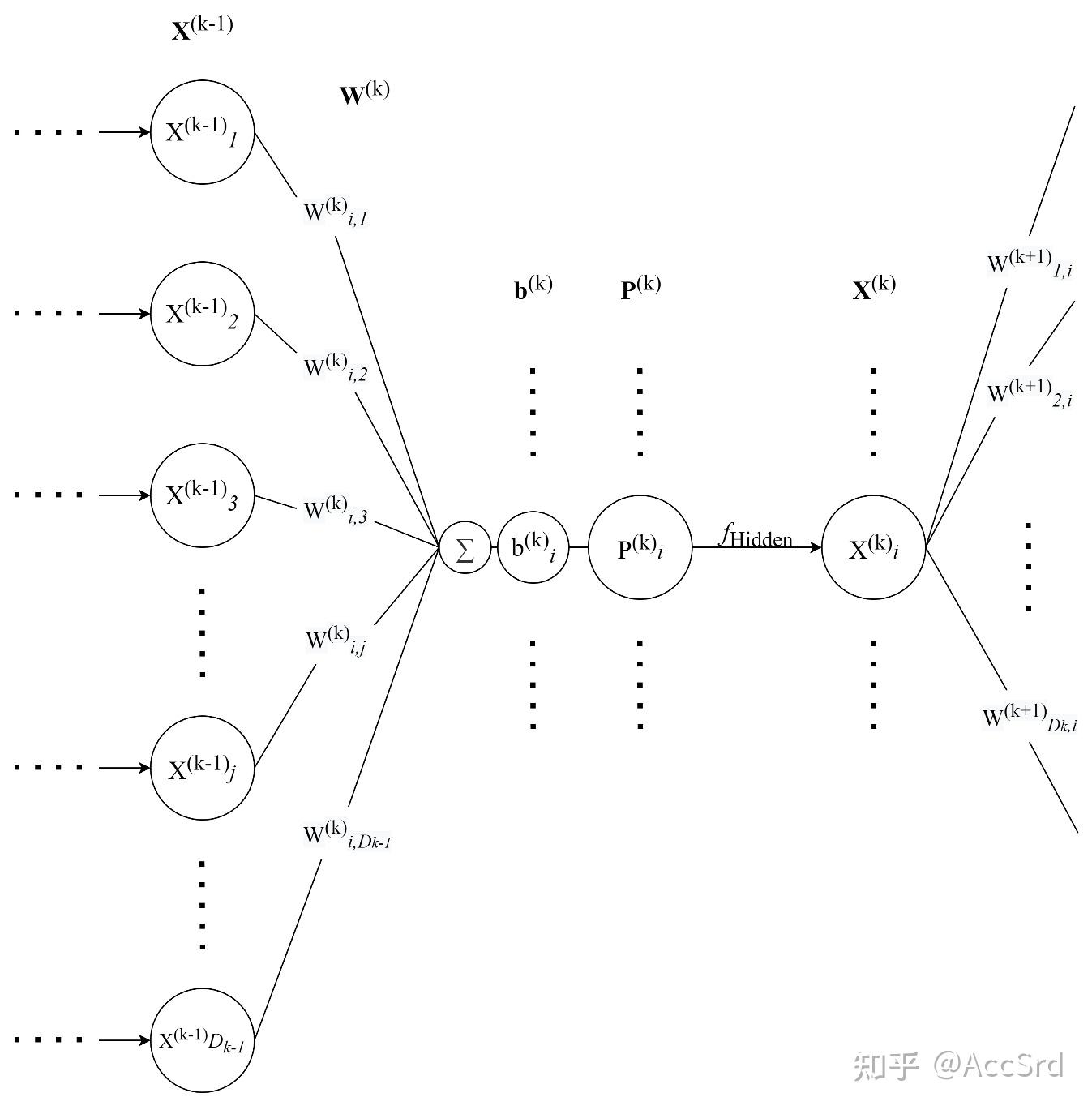
隐藏层内传递

Pk=WkXk−1+bk=[∑j=1Dk−1W1,jkXjk−1+b1k∑j=1Dk−1W2,jkXjk−1+b2k⋮∑j=1Dk−1Wi,jkXjk−1+bik⋮∑j=1Dk−1WDk,jkXjk−1+bDkk]Dk×1=[P1kP2k⋮Pik⋮PDkk]Dk×1\mathbf{P}^k=\mathbf{W}^k\mathbf{X}^{k-1}+\mathbf{b}^k= \begin{bmatrix} \sum_{j=1}^{D_{k-1}}W_{1,j}^kX_j^{k-1}+b_1^k\\ \sum_{j=1}^{D_{k-1}}W_{2,j}^kX_j^{k-1}+b_2^k\\ \vdots\\ \sum_{j=1}^{D_{k-1}}W_{i,j}^kX_j^{k-1}+b_i^k\\ \vdots\\ \sum_{j=1}^{D_{k-1}}W_{D_k,j}^kX_j^{k-1}+b_{D_k}^k\\ \end{bmatrix}_{D_k\times1} =\begin{bmatrix} P_1^k\\ P_2^k\\ \vdots\\ P_i^k\\ \vdots\\ P_{D_k}^k\\ \end{bmatrix}_{D_k\times1}

当采用 Batch 进行训练时：

Pk=WkXk−1+bk=[∑j=1Dk−1W1,jkXjb1k−1+b1k⋯∑j=1Dk−1W1,jkXjbDbk−1+b1k∑j=1Dk−1W2,jkXjb1k−1+b2k⋯∑j=1Dk−1W2,jkXjbDbk−1+b2k⋮⋮⋮∑j=1Dk−1Wi,jkXjb1k−1+bik⋯∑j=1Dk−1Wi,jkXjbDbk−1+bik⋮⋮⋮∑j=1Dk−1WDk,jkXjb1k−1+bDkk⋯∑j=1Dk−1WDk,jkXjbDbk−1+bDkk]Dk×Db=[P1b1k⋯P1bDbkP2b1k⋯P2bDbk⋮⋮⋮Pib1k⋯PibDbk⋮⋮⋮PDkb1k⋯PDkbDbk]Dk×Db\begin{aligned} \mathbf{P}^k=\mathbf{W}^k\mathbf{X}^{k-1}+\mathbf{b}^k&= \begin{bmatrix} \sum_{j=1}^{D_{k-1}}W_{1,j}^kX_{jb_1}^{k-1}+b_1^k&\cdots&\sum_{j=1}^{D_{k-1}}W_{1,j}^kX_{jb_{D_b}}^{k-1}+b_1^k\\ \sum_{j=1}^{D_{k-1}}W_{2,j}^kX_{jb_1}^{k-1}+b_2^k&\cdots&\sum_{j=1}^{D_{k-1}}W_{2,j}^kX_{jb_{D_b}}^{k-1}+b_2^k\\ \vdots&\vdots&\vdots\\ \sum_{j=1}^{D_{k-1}}W_{i,j}^kX_{jb_1}^{k-1}+b_i^k&\cdots&\sum_{j=1}^{D_{k-1}}W_{i,j}^kX_{jb_{D_b}}^{k-1}+b_i^k\\ \vdots&\vdots&\vdots\\ \sum_{j=1}^{D_{k-1}}W_{D_k,j}^kX_{jb_1}^{k-1}+b_{D_k}^k&\cdots&\sum_{j=1}^{D_{k-1}}W_{D_k,j}^kX_{jb_{D_b}}^{k-1}+b_{D_k}^k\\ \end{bmatrix}_{D_k\times D_b}\\ &=\begin{bmatrix} P_{1b_1}^k&\cdots&P_{1b_{D_b}}^k\\ P_{2b_1}^k&\cdots&P_{2b_{D_b}}^k\\ \vdots&\vdots&\vdots\\ P_{ib_1}^k&\cdots&P_{ib_{D_b}}^k\\ \vdots&\vdots&\vdots\\ P_{D_kb_1}^k&\cdots&P_{D_kb_{D_b}}^k\\ \end{bmatrix}_{D_k\times D_b} \end{aligned}

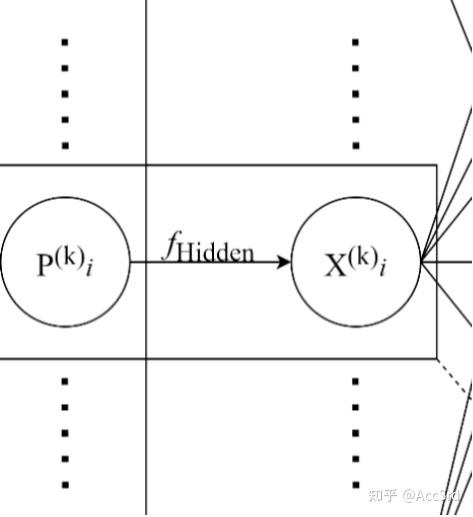
隐藏层间传递

Xk=f(Pk)=[f(P1k)f(P2k)⋮f(PDkk)]Dk×1\mathbf{X}^k=f(\mathbf{P}^k)=\begin{bmatrix} f(P_1^k)\\ f(P_2^k)\\ \vdots\\ f(P_{D_k}^k)\\ \end{bmatrix}_{D_k\times1}

当采用 Batch 进行训练时：

Xk=f(Pk)=[f(P1b1k)f(P1b2k)⋯f(P1bDbk)f(P2b1k)f(P2b2k)⋯f(P2bDbk)⋮⋮⋱⋮f(PDkb1k)f(PDkb2k)⋯f(PDkbDbk)]Dk×Db\mathbf{X}^k=f(\mathbf{P}^k)=\begin{bmatrix} f(P_{1b_1}^k)&f(P_{1b_2}^k)&\cdots&f(P_{1b_{D_b}}^k)\\ f(P_{2b_1}^k)&f(P_{2b_2}^k)&\cdots&f(P_{2b_{D_b}}^k)\\ \vdots&\vdots&\ddots&\vdots\\ f(P_{D_kb_1}^k)&f(P_{D_kb_2}^k)&\cdots&f(P_{D_kb_{D_b}}^k)\\ \end{bmatrix}_{D_k\times D_b}

其中 f(⋅)f(\cdot) 为两隐藏层间的激活函数（一般是 Element-wise 的）。

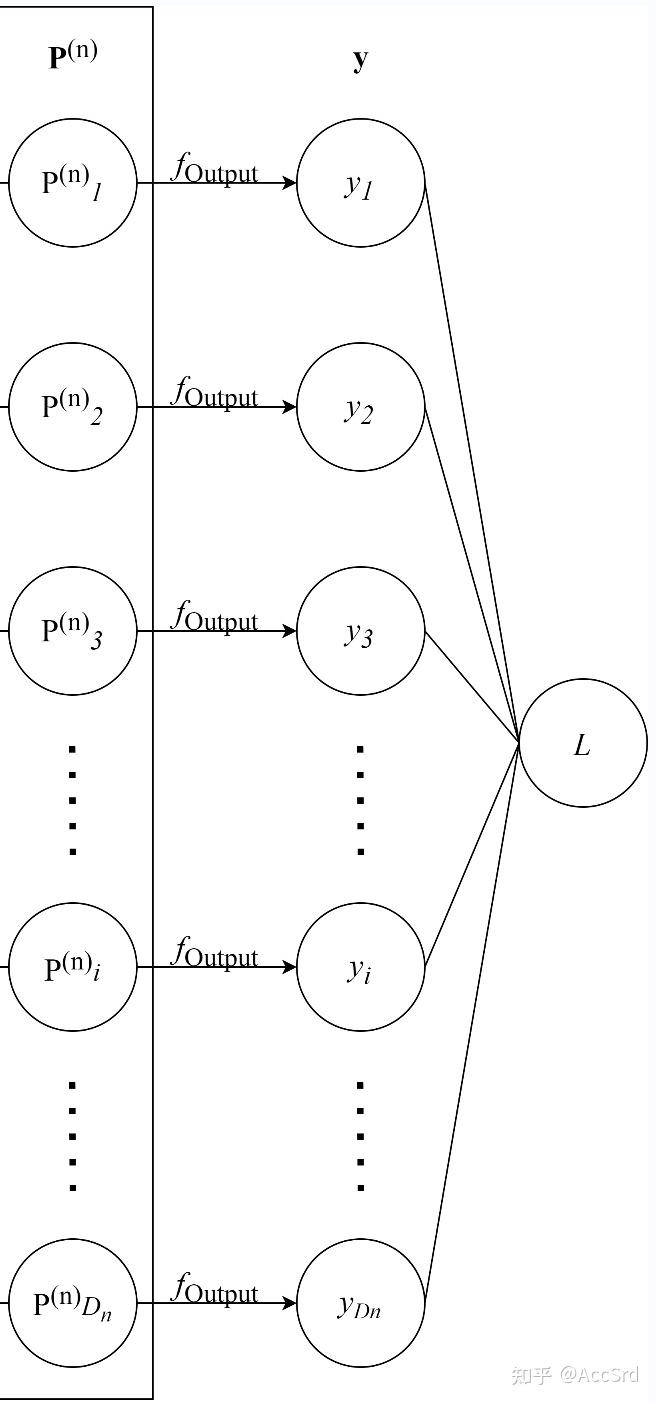
输出层

输出层（第 nn 层）的参数向量 Pn\mathbf{P}^n 通过 foutputf_{\text{output}} 得到结果。

  • y\mathbf{y} 为网络预测的分类结果，Y\mathbf{Y} 为输入数据标注的真实标签

y=foutput(Pn), L=Loss(Y,y)\mathbf{y}=f_{\text{output}}(\mathbf{P}^n),\ \mathcal{L}=\text{Loss}(\mathbf{Y},\mathbf{y})

反向传播（BP）与梯度下降

反向传播

∂L∂Pn=∂L∂y⊙foutput′(Pn)T\frac{\partial\mathcal{L}}{\partial\mathbf{P}^n}=\frac{\partial\mathcal{L}}{\partial\mathbf{y}}\odot f'_{\text{output}}(\mathbf{P}^n)^T

{∂L∂Pk=(∂L∂Pk+1⋅Wk+1)⊙f′(Pk)T∂L∂Wk=Xk−1⋅∂L∂Pk∂L∂bk=∂L∂Pk,0≤k<n\begin{dcases} \frac{\partial\mathcal{L}}{\partial\mathbf{P}^k}=\left(\frac{\partial\mathcal{L}}{\partial\mathbf{P}^{k+1}}\cdot\mathbf{W}^{k+1}\right)\odot f'(\mathbf{P}^k)^T\\ \frac{\partial\mathcal{L}}{\partial\mathbf{W}^k}=\mathbf{X}^{k-1}\cdot\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k}\\ \frac{\partial\mathcal{L}}{\partial\mathbf{b}^k}=\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k} \end{dcases} ,\quad 0\le k<n

当采用 Batch（同时训练多个数据）进行训练时，偏置梯度更新为以下式子：

∂L∂bk=J1×Db⋅∂L∂Pk\frac{\partial\mathcal{L}}{\partial\mathbf{b}^k}=\mathbf{J}_{1\times D_b}\cdot\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k}

梯度下降

{W(s+1)k=W(s)k−α⋅∂L∂W(s)kTb(s+1)k=b(s)k−α⋅∂L∂b(s)kT,0≤k<n\begin{dcases} \mathbf{W}^k_{(s+1)}=\mathbf{W}^k_{(s)}-\alpha\cdot\frac{\partial\mathcal{L}}{\partial\mathbf{W}^k_{(s)}}^T\\ \mathbf{b}^k_{(s+1)}=\mathbf{b}^k_{(s)}-\alpha\cdot\frac{\partial\mathcal{L}}{\partial\mathbf{b}^k_{(s)}}^T \end{dcases} ,\quad 0\le k<n

其中：

  • (s)(s) 和 (s+1)(s+1) 分别表示当前状态和下一状态
  • α\alpha 为学习率（Learning rate）
  • DkD_k 为第 kk 层网络中的神经元个数
数学推导

描述反向传播与梯度下降更新过程：

  1. 计算输出层的 ∂L∂Pn\frac{\partial\mathcal{L}}{\partial\mathbf{P}^n} 作为初始状态
    1. 计算本层的 Pn\mathbf{P}^n（前向传播），代入输出函数的导数得到一个列向量，将其转置为行向量
    2. 计算 ∂L∂y\frac{\partial\mathcal{L}}{\partial\mathbf{y}}（相当于行向量中对每个 yiy_i 分别求偏导）

      1. MSE（均方误差）的梯度为：

        L=1Dn∑i=1Dn(Yi−yi)2\mathcal{L}=\frac{1}{D_n}\sum^{D_n}_{i=1}(Y_i-y_i)^2

        ∂L∂y=[−2Y1+2y1Dn−2Y2+2y2Dn⋯−2YDn+2yDnDn]{\frac{\partial\mathcal{L}}{\partial\mathbf{y}}}=\left[ \begin{darray}{ccc} \frac{-2Y_1+2y_1}{D_n}&\frac{-2Y_2+2y_2}{D_n}&\cdots&\frac{-2Y_{D_n}+2y_{D_n}}{D_n} \end{darray}\right]

      2. Cross-Entropy Error（交叉熵损失）的梯度为：

        L=∑i=1DnYilog⁡yi\mathcal{L}=\sum^{D_n}_{i=1}Y_i\log{y_i}

        ∂L∂y=[Y1y1Y2y2⋯YDnyDn]{\frac{\partial\mathcal{L}}{\partial\mathbf{y}}}=\left[ \begin{darray}{ccc} \frac{Y_1}{y_1}&\frac{Y_2}{y_2}&\cdots&\frac{Y_{D_n}}{y_{D_n}} \end{darray}\right]

    3. a. 与 b. 点乘得到 ∂L∂Pn\frac{\partial\mathcal{L}}{\partial\mathbf{P}^n}
  2. 递推计算上一层的 ∂L∂Pk\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k}
    1. 计算本层的 Pk\mathbf{P}^k（前向传播），代入激活函数的导数
    2. 下一层的 ∂L∂Pk+1\frac{\partial\mathcal{L}}{\partial\mathbf{P}^{k+1}} 与下一层的权值 Wk+1\mathbf{W}^{k+1} 相乘，再与 f′(P(s)k)Tf'(\mathbf{P}^k_{(s)})^T 点乘得到本层 ∂L∂Pk\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k}
  3. 递推计算上一层的权值梯度 ∂L∂Wk\frac{\partial\mathcal{L}}{\partial\mathbf{W}^k}
    1. 本层输入 Xk−1\mathbf{X}^{k-1} 乘以 ∂L∂Pk\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k}
  4. 递推计算上一层的偏置梯度 ∂L∂bk\frac{\partial\mathcal{L}}{\partial\mathbf{b}^k}
    1. 单数据训练时，为本层 ∂L∂Pk\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k}
    2. Batch 训练时，为本层 J1×Db⋅∂L∂Pk\mathbf{J}_{1\times D_b}\cdot\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k}（相当于 ∂L∂Pk\frac{\partial\mathcal{L}}{\partial\mathbf{P}^k} 每行求和）
  5. 梯度下降更新上一层的权值 W(s+1)k\mathbf{W}^k_{(s+1)} 与偏置 b(s+1)k\mathbf{b}^k_{(s+1)}
    1. 权值更新为原权值减去学习率乘以权值梯度的转置 ∂L∂W(s)kT\frac{\partial\mathcal{L}}{\partial\mathbf{W}^k_{(s)}}^T
    2. 偏置更新为原偏置减去学习率乘以偏置梯度的转置 ∂L∂b(s)kT\frac{\partial\mathcal{L}}{\partial\mathbf{b}^k_{(s)}}^T
  6. 重复 2. - 5. 直至更新至第一层
  7. 重复 1. - 6. 直至损失函数小于事先给定的阈值 / 达到迭代次数

Numpy 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
import numpy as np
import matplotlib.pyplot as plt

MSE = lambda y, t : np.mean((y - t) ** 2)
MSE_f = lambda y, Y : 2 * (y - Y) / Y.shape[0]
CEE = lambda y, t : np.sum(y * np.log(t))
CEE_f = lambda y, Y : Y / y

class Layer:
    def __init__(self, input_n, param):
        self.input_n = input_n
        self.n = param['n']
        self.weights = np.random.uniform(size = (self.n, input_n)) * 0.01 # Uniform Initialization
        self.biases = np.zeros((self.n, 1))
        self.learning_rate = param['learning_rate']
        self.sigma = param['sigma']
        self.sigma_d = param['sigma_d']

    def forward(self, input):
        self.output = self.sigma(self.weights @ input + self.biases)

    def update(self, input):
        self.weights -= self.learning_rate * (input @ self.error_term).T
        self.biases -= self.learning_rate * (np.ones((1, self.error_term.shape[0])) @ self.error_term).T 

class All_Connect_Layer(Layer):
    def __init__(self, input_n, param):
        super().__init__(input_n, param)

    def calc_loss(self, next_error_term, next_weights):
        error = next_error_term @ next_weights
        self.error_term = error * self.sigma_d(self.output).T

class Output_Layer(Layer):
    def __init__(self, input_n, param):
        super().__init__(input_n, param)

    def calc_loss(self, y, error_f):
        error = error_f(self.output, y).T
        self.error_term = error * self.sigma_d(self.output).T

class MLP:
    def __init__(self, layer_array, x, y, error_f, seed):
        assert y.shape[0] == layer_array[-1]['n']
        self.x = x
        self.y = y
        self.layers = []
        self.output_n = y.shape[0]
        self.error_f = error_f
        self.batch_size = 1

        np.random.seed(seed)

        self.layers.append(All_Connect_Layer(x.shape[0], layer_array[0]))
        if len(layer_array) > 2:
            for i in range(1, len(layer_array) - 1):
                self.layers.append(All_Connect_Layer(layer_array[i-1]['n'], layer_array[i]))
        self.layers.append(Output_Layer(layer_array[-2]['n'], layer_array[-1]))

    def iterate(self):
        random_indices = np.random.permutation(self.x.shape[1])
        x_random, y_random = self.x[:, random_indices], self.y[:, random_indices]
        for x, y in zip([x_random], [y_random]):
            # Forward
            self.layers[0].forward(x)
            for i in range(1, len(self.layers)):
                self.layers[i].forward(self.layers[i-1].output)
            # Calc_loss
            self.layers[-1].calc_loss(y, self.error_f)
            for i in range(len(self.layers) - 2, -1, -1):
                self.layers[i].calc_loss(self.layers[i+1].error_term, self.layers[i+1].weights)
            # Update
            self.layers[0].update(x)
            for i in range(1, len(self.layers)):
                self.layers[i].update(self.layers[i-1].output)
            # Output
            self.output = self.layers[-1].output
        return x_random, y_random

    def training(self, epochs, test, label, loss_f):
        plot_epoch, plot_training, plot_test = [], [], []
        for epoch in range(epochs):
            x_random, y_random = self.iterate()
            plot_epoch.append(epoch)
            output = self.test(x_random)
            train_loss = loss_f(y_random, output)
            plot_training.append(train_loss)
            result = self.test(test)
            test_loss = loss_f(label, result)
            plot_test.append(test_loss)
            print(f"Epoch {epoch}, Train Loss: {train_loss:.4f}, Test Loss: {test_loss:.4f}")

        plt.plot(plot_epoch, plot_training, label = 'Train')
        plt.plot(plot_epoch, plot_test, color = 'orange', label = 'Test')
        plt.title('Loss')
        plt.legend()
        plt.show()

    def test(self, x):
        self.layers[0].forward(x)
        for i in range(1, len(self.layers)):
            self.layers[i].forward(self.layers[i-1].output)
        return self.layers[-1].output

优化策略

Xavier 初始化

为了尽量达到输入、输出方差一致的目标而采用的初始化办法。

激活函数 Sigmoid ReLU Tanh
均匀分布 （取值上下限） ±6Dn−1+Dn\pm\sqrt{\frac{6}{D_{n-1}+D_n}} ±12Dn−1+Dn\pm\sqrt{\frac{12}{D_{n-1}+D_n}} ±46Dn−1+Dn\pm4\sqrt{\frac{6}{D_{n-1}+D_n}}
高斯分布 （取值标准差） 2Dn−1+Dn\sqrt{\frac{2}{D_{n-1}+D_n}} 4Dn−1+Dn\sqrt{\frac{4}{D_{n-1}+D_n}} 42Dn−1+Dn4\sqrt{\frac{2}{D_{n-1}+D_n}}

数据标准化

X′=X−μ⃗σ⃗\mathbf{X}'=\frac{\mathbf{X}-\vec{\mu}}{\vec{\sigma}}

Batch Normalization

通过归一化手段，将每层输入强行拉回均值 0 方差为 1 的标准正态分布，这样使得激活输入值分布在非线性函数梯度敏感区域，从而避免梯度消失问题，大大加快训练速度。

优化激活函数

激活函数

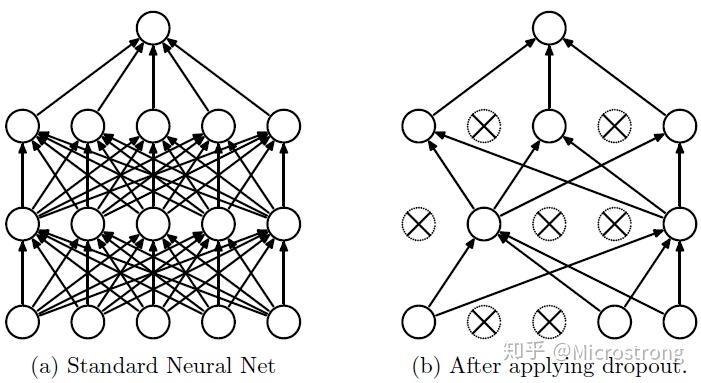
Dropout

在前向传播的时候，让某个神经元的激活值以一定的概率 pp 停止工作，可以使模型泛化性更强。

rk−1=Bernoulli(p),dim⁡rk−1=dim⁡Xk−1X′k−1=rk−1⊙Xk−11−pPk=WkX′k−1+bk\begin{gathered} \mathbf{r}^{k-1}=\text{Bernoulli}(p),\quad \dim{\mathbf{r}^{k-1}}= \dim{\mathbf{X}^{k-1}}\\ \mathbf{X'}^{k-1}=\frac{\mathbf{r}^{k-1}\odot\mathbf{X}^{k-1}}{1-p}\\ \mathbf{P}^k=\mathbf{W}^k\mathbf{X'}^{k-1}+\mathbf{b}^k \end{gathered}

反向传播时，只更新本轮正在工作的神经元权值。

为了维持权重参数，在前向传播时对剩下的神经元乘以补偿系数1/(1−p)1/(1-p)。

测试时不进行 Dropout。

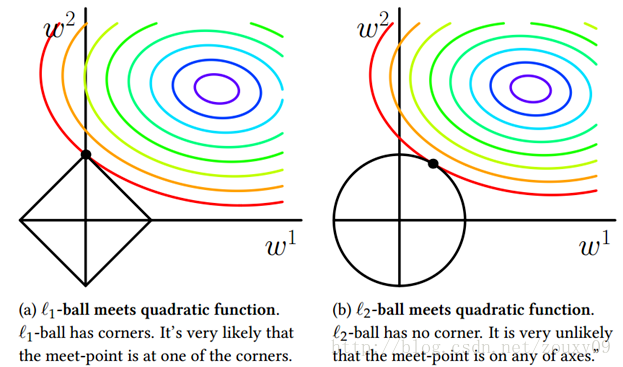
权重衰退（L2 正则化）

权重衰退的目的是让模型权重减小（控制在某一个范围内），以此来减小模型的复杂性，从而抑制过拟合。

L=L0+λ2∣∣W∣∣2⇒W(s+1)k=W(s)k−α⋅∂L∂W(s)kT=W(s)k−α⋅(∂L0∂W(s)kT+λW(s)k)\begin{aligned} \mathcal{L}&=\mathcal{L}_0+\frac{\lambda}{2}||\mathbf{W}||^2\\ \Rightarrow\mathbf{W}^k_{(s+1)}&=\mathbf{W}^k_{(s)}-\alpha\cdot\frac{\partial\mathcal{L}}{\partial\mathbf{W}^k_{(s)}}^T\\ &=\mathbf{W}^k_{(s)}-\alpha\cdot\left(\frac{\partial\mathcal{L}_0}{\partial\mathbf{W}^k_{(s)}}^T+\lambda\mathbf{W}^k_{(s)}\right) \end{aligned}

Numpy 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
import numpy as np
import matplotlib.pyplot as plt

MSE = lambda y, t : np.mean((y - t) ** 2)
MSE_f = lambda y, Y : 2 * (y - Y) / Y.shape[0]
CEE = lambda y, t : np.sum(y * np.log(t))
CEE_f = lambda y, Y : Y / y

class Layer:
    def __init__(self, input_n, param):
        self.input_n = input_n
        self.n = param['n']
        self.weights = np.random.randn(self.n, input_n) * np.sqrt(4. / (input_n + self.n)) # Xavier Initialization
        self.biases = np.zeros((self.n, 1))
        self.learning_rate = param['learning_rate']
        self.sigma = param['sigma']
        self.sigma_d = param['sigma_d']
        self.weight_decay = param['weight_decay']
        self.dropout_rate = param['dropout']
        self.dropout_array = np.tile(np.random.binomial(1, 1 - self.dropout_rate, input_n), (self.n, 1)) # Neuron-wise Dropout

    def forward(self, input, is_final = False):
        dropout_param = 0 if is_final else self.dropout_rate
        self.output = self.sigma((self.weights * self.dropout_array / (1 - dropout_param)) @ input + self.biases)

    def update(self, input):
        self.weights -= self.learning_rate * (self.weights * self.weight_decay + (input @ self.error_term).T) * self.dropout_array
        self.biases -= self.learning_rate * (np.ones((1, self.error_term.shape[0])) @ self.error_term).T
        self.dropout_array = np.tile(np.random.binomial(1, 1 - self.dropout_rate, self.input_n), (self.n, 1))

class All_Connect_Layer(Layer):
    def __init__(self, input_n, param):
        super().__init__(input_n, param)

    def calc_loss(self, next_error_term, next_weights):
        error = next_error_term @ next_weights
        self.error_term = error * self.sigma_d(self.output).T

class Output_Layer(Layer):
    def __init__(self, input_n, param):
        super().__init__(input_n, param)

    def calc_loss(self, y, error_f):
        error = error_f(self.output, y).T
        self.error_term = error * self.sigma_d(self.output).T

class MLP:
    def __init__(self, layer_array, x, y, error_f, batch_size, seed):
        assert y.shape[0] == layer_array[-1]['n']
        self.x = x
        self.y = y
        self.layers = []
        self.output_n = y.shape[0]
        self.error_f = error_f
        self.batch_size = batch_size

        np.random.seed(seed)

        self.layers.append(All_Connect_Layer(x.shape[0], layer_array[0]))
        if len(layer_array) > 2:
            for i in range(1, len(layer_array) - 1):
                self.layers.append(All_Connect_Layer(layer_array[i-1]['n'], layer_array[i]))
        self.layers.append(Output_Layer(layer_array[-2]['n'], layer_array[-1]))

    def gen_batch(self, x, y):
        x_batch, y_batch = [], []
        for i in range(self.batch_size):
            indices = np.arange(i, x.shape[1], self.batch_size)
            x_batch.append(x[:, indices])
            y_batch.append(y[:, indices])
        return x_batch, y_batch

    def iterate(self):
        random_indices = np.random.permutation(self.x.shape[1])
        x_random, y_random = self.x[:, random_indices], self.y[:, random_indices]
        x_batch, y_batch = self.gen_batch(x_random, y_random)
        for x, y in zip(x_batch, y_batch):
            # Forward
            self.layers[0].forward(x)
            for i in range(1, len(self.layers)):
                self.layers[i].forward(self.layers[i-1].output)
            # Calc_loss
            self.layers[-1].calc_loss(y, self.error_f)
            for i in range(len(self.layers) - 2, -1, -1):
                self.layers[i].calc_loss(self.layers[i+1].error_term, self.layers[i+1].weights)
            # Update
            self.layers[0].update(x)
            for i in range(1, len(self.layers)):
                self.layers[i].update(self.layers[i-1].output)
            # Output
            self.output = self.layers[-1].output
        return x_random, y_random

    def training(self, epochs, test, label, loss_f):
        plot_epoch, plot_training, plot_test = [], [], []
        for epoch in range(epochs):
            x_random, y_random = self.iterate()
            plot_epoch.append(epoch)
            output = self.test(x_random)
            train_loss = loss_f(y_random, output)
            plot_training.append(train_loss)
            result = self.test(test)
            test_loss = loss_f(label, result)
            plot_test.append(test_loss)
            print(f"Epoch {epoch}, Train Loss: {train_loss:.4f}, Test Loss: {test_loss:.4f}")

        plt.plot(plot_epoch, plot_training, label = 'Train')
        plt.plot(plot_epoch, plot_test, color = 'orange', label = 'Test')
        plt.title('Loss')
        plt.legend()
        plt.show()

    def test(self, x, is_final = False):
        if is_final:
            for layer in self.layers:
                layer.dropout_array = np.ones((layer.n, layer.input_n))
        self.layers[0].forward(x)
        for i in range(1, len(self.layers)):
            self.layers[i].forward(self.layers[i-1].output, is_final)
        return self.layers[-1].output